Nonequilibrium statistical mechanics

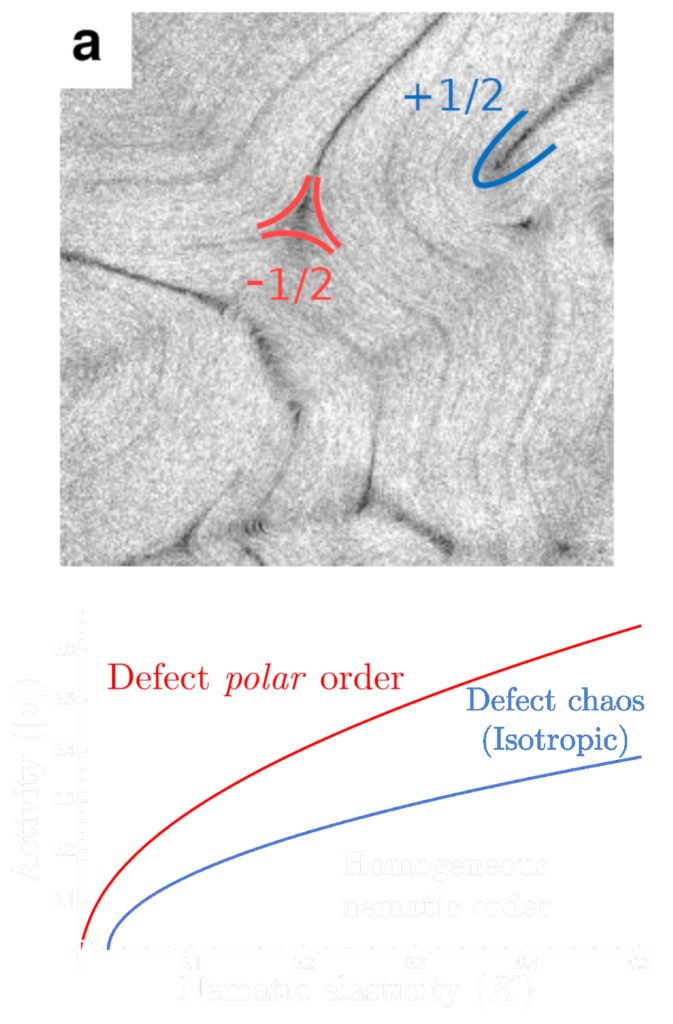
Active fluids, such as bacterial suspensions, cytoskeletal extracts, cellular aggregates, etc., often exhibit orientational order accompanied by spatiotemporally chaotic dynamics and spontaneous flows. How is order maintained or destroyed by nonequilibrium driving, flows, and fluctuations? A tractable approach is to focus on the dynamics of singular excitations in orientational order called topological defects that are familiar from condensed matter systems, e.g., superfluids, magnets, etc. In active fluids, defects often become self-propelled and self-stir the liquid. We have formulated an effective particle-like description of active defects and shown how their unbinding and proliferation leads to nonequilibrium phase transitions and novel states of order. Open questions include – How does nonequilibrium activity allow new kinds of robust topological states? What is the statistical mechanics of fluctuations, flow and defects in active fluids? What role do nonreciprocal interactions and motility play in phase transitions and universality?

Confined, complex & curved environments

From migrating wildebeest herds in the Savannah to crawling cells in the crypts and villi of our gut, collective motion often occurs in complex, heterogeneous, and curved environments. What impact do the mechanical and geometric features of the environment have on the collective movement of active agents? How do surface curvature, roughness, obstacles, etc., disrupt and channelize active flows? What happens when the environment is dynamic, responsive, and time-varying such as in a viscoelastic fluid? In our work we have shown how surface curvature can robustly confine topologically protected density waves in flocking liquids, in a manner akin to edge states in quantum Hall systems. Disorder due to a random distribution of obstacles, when strong enough, can force active flows to break-up into a frozen array of flowing vortices. This unusual glassy phase intervenes between the ordered liquid and disordered gas in a two-step melting process and is analogous to vortex glass phases seen in dirty superconductors. We have also explored the impact of dissolved polymers on the collective swimming of bacteria. Remarkably, we find that polymer viscoelasticity calms turbulent bacterial flows on macroscales and can generate dramatic fluid oscillations due to a delayed elastic response of the fluid. Understanding how substrate and environmental manipulations can be used to control active flows, channel excitations, and exploring the relevance of these effects in physiology are current areas of open research – also see Inverse problems & control and Biological physics.